QUANTIQUE (OPTIQUE)

QUANTIQUE (OPTIQUE)

La nature de la lumière a fait l’objet depuis toujours de débats passionnés. Dès le XVII^e siècle s’affrontaient les tenants d’une conception ondulatoire, comme Huygens, et les partisans d’une théorie corpusculaire, comme Newton puis Laplace. Au XIX^e siècle, les travaux de Fresnel, de Young puis de Maxwell aboutirent à l’élaboration de la théorie classique de la lumière, identifiée à une onde de champ électromagnétique, qui expliquait la quasi-totalité des phénomènes optiques connus. Cette vision purement ondulatoire de la lumière ne triompha pas très longtemps: au début du XX^e siècle, les travaux de Planck sur le rayonnement thermique puis d’Einstein sur l’effet photoélectrique permirent l’émergence des premiers concepts quantiques et l’introduction des quanta de lumière: les photons. Mais le problème était loin d’être réglé définitivement: comment concilier cette vision corpusculaire de la lumière avec ses propriétés manifestement ondulatoires, telles qu’elles apparaissent dans les phénomènes d’interférences? Ce problème essentiel resta sans réponse pendant de nombreuses années.

Pendant ce temps, la théorie quantique se développait à partir d’autres branches de la physique, notamment la physique atomique. La mécanique quantique, élaborée dans les années 1920, permit de calculer précisément les énergies quantifiées des atomes, de la matière en général, mais aussi du champ électromagnétique.

La mécanique quantique montrait aussi qu’on pouvait très bien expliquer l’effet photoélectrique sans faire appel aux photons! On obtient en effet toutes les lois de l’effet photoélectrique en calculant l’interaction entre la matière quantifiée et le champ électromagnétique classique, donc non quantifié. La quantification de la lumière et l’explication des phénomènes en termes de photons ne semblaient donc pas indispensables à la compréhension des phénomènes optiques. Certains en venaient même à douter de l’existence réelle de cette particule.

L’invention du laser, dans les années 1960, déclencha un effort de recherche considérable sur les aspects spécifiquement quantiques des phénomènes lumineux. Les théoriciens montrèrent qu’il existait des phénomènes en optique qui, à la différence de l’effet photoélectrique, ne pouvaient pas être décrits en termes d’ondes électromagnétiques classiques. À partir de 1977, une série de très belles expériences confirma ces prédictions.

On peut maintenant expliquer l’ensemble des phénomènes lumineux observés à ce jour dans le cadre de l’optique quantique, qui a enfin permis de réconcilier Newton et Huyghens: pour la première fois, on dispose d’une théorie capable de rendre compte de manière unifiée de l’ensemble des phénomènes observés. Certaines expériences sont mieux comprises en ayant recours à des images classiques en termes de corpuscules, d’autres en termes d’ondes, mais toutes sont calculables de manière non ambiguë dans le cadre de la théorie quantique du rayonnement.

Celle-ci n’est pas seulement une synthèse entre les deux anciennes conceptions. Elle contient aussi des effets nouveaux qui ne sont réductibles ni à l’une ni à l’autre de ces deux descriptions complémentaires. Mentionnons en particulier l’importance du concept de fluctuations quantiques du rayonnement, et notamment des fluctuations du vide, qui jouent un rôle fondamental dans l’interprétation de nombreux phénomènes.

En retour, le développement de l’optique quantique a permis de mieux comprendre les concepts de base de la théorie quantique, comme les relations d’incertitude de Heisenberg et la théorie de la mesure. L’optique est devenue un des domaines privilégiés où l’on peut tester expérimentalement des points subtils de la théorie quantique. Mentionnons enfin que ces progrès récents ne sont pas seulement conceptuels: ils ouvrent la voie à l’augmentation de la sensibilité des mesures optiques, par exemple dans les expériences extraordinairement délicates de détection par interférométrie optique des ondes de gravitation.

1. Description classique et quantique d’une onde lumineuse

Considérons une onde plane monochromatique de pulsation 諸 se propageant parallèlement à l’axe Oz . En théorie classique, le champ électrique de cette onde s’écrit ^{[cf. LUMIÈRE - Optique]}:

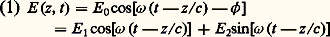(c : vitesse de la lumière). Nous représenterons cette onde dans un plan, appelé « plan de Fresnel », par un point M dont les coordonnées polaires sont l’amplitude E ⁰ et la phase à l’origine 﨏 de l’onde (fig. 1 a). On appelle composantes de quadrature de l’onde les coordonnées cartésiennes E ¹ et E ² du point M. L’évolution temporelle (ou spatiale le long de l’axe Oz ) de cette onde correspond à une rotation du vecteur OM autour de l’origine avec une période temporelle 2 神/ 諸 (ou une période spatiale = 2 神c/ 諸). Mentionnons enfin que l’énergie de l’onde est proportionnelle au carré E ²⁰ de l’amplitude, soit encore à la quantité E ²¹ + E ²². L’état de l’onde est entièrement déterminé par la donnée du point M, c’est-à-dire des coordonnées E ¹ et E ². Rien n’empêche en théorie classique de définir ces grandeurs avec une précision arbitrairement grande.

Le passage à la description quantique de l’onde se fait de la même manière que pour la particule matérielle (cf. mécanique QUANTIQUE): il consiste à remplacer les variables E ¹ et E ² du système par des opérateurs (ou observables), notées E¹ et E², agissant sur l’espace des états du champ. On sait que les propriétés quantiques d’une particule sont directement reliées au fait qu’entre les observables X et P associées à sa position x et à sa quantité de mouvement p existe la relation de commutation canonique (cf. mécanique QUANTIQUE):

(h : constante de Planck divisée par 2 神, I: opérateur identité). De même, les propriétés quantiques du rayonnement proviennent de l’existence d’une relation de commutation canonique entre E¹ et E²: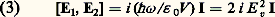

( 﨎⁰: permittivité du vide, V: volume dans lequel on définit l’onde plane). À partir de la relation (3), on montre que l’énergie de l’onde électromagnétique prend des valeurs quantifiées , égales à (n + 1/2)h 諸, où n est un nombre entier positif. L’énergie de l’onde est, au terme constant (1/2)h 諸 près, celle de n quanta d’énergie h 諸: les photons . C’est ainsi qu’apparaît l’aspect corpusculaire de l’onde lumineuse ^{[cf. PHOTON]}. Si on calcule l’impulsion du champ, on la trouve égale à nh 諸/c . On peut donc aussi attribuer à chacun des n photons de l’onde une impulsion égale à h 諸/c.

La relation de commutation (3) a une autre conséquence importante, concernant la mesure du champ électrique de l’onde ^{[cf. MESURE]}. Elle implique qu’il n’existe pas d’état du champ dans lequel les composantes de quadrature E ¹ et E ² sont connues toutes deux avec une précision absolue. De même que la relation (2) implique la célèbre relation de Heisenberg x p 閭 h /2, de même la relation (3) implique l’inégalité:

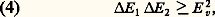où E ¹ et E ² représentent les dispersions des résultats de mesure de E ¹ et E ² pour une onde préparée dans un état quantique quelconque. On ne peut donc pas caractériser l’état quantique du système par un point dans le plan de Fresnel, mais par une surface d’extension finie , centrée sur le point M dont les coordonnées sont les valeurs moyennes des mesures de E ¹ et E ², et dont les dimensions transverses donnent les dispersions E ¹ et E ² (fig. 1 b). L’aspect quantique de la lumière se caractérise donc par l’apparition de ce « flou » sur la connaissance de M, qui est la manifestation de l’existence de fluctuations quantiques dans l’onde.

Une manière moins rigoureuse, mais plus parlante, de caractériser ces fluctuations est de récrire la relation (4) en termes de dispersion sur les mesures de la phase 﨏, de l’énergie H , et du nombre de photons n. On trouve:

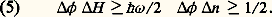Cette relation illustre la complémentarité entre descriptions corpusculaire et ondulatoire de l’onde. En effet, considérons un état de la lumière dans lequel la phase est déterminée avec précision ( 﨏 麗麗 2 神). Le même état aura d’après les inégalités (5) une grande dispersion sur l’énergie et sur le nombre de photons qu’il contient. L’aspect corpusculaire de cet état sera peu apparent. Inversement, un état dans lequel le nombre de photons est bien déterminé aura d’après (5) une très grande dispersion de phase et sera caractérisé par une faible cohérence temporelle ^{[cf. OPTIQUE - Optique cohérente]}. Il faut enfin signaler que, d’après la première inégalité de (5), la limite imposée par la relation de Heisenberg est d’autant moins contraignante que 諸 est petit: les effets quantiques sont négligeables dans le domaine des ondes hertziennes ( 諸 年 10⁷ Hz ), et dominants dans le domaine des rayons X ( 諸 年 10¹⁷ Hz ). La lumière visible ( 諸 年 10¹⁴ Hz ) se place dans une région intermédiaire où effets ondulatoires et effets corpusculaires sont également importants.

Un photodétecteur placé sur le trajet de l’onde permet de mesurer le flux énergétique instantané de celle-ci. Les fluctuations quantiques de l’onde se manifestent alors comme des variations temporelles erratiques du photocourant mesuré, c’est-à-dire comme un bruit de fond dans la mesure. L’optique est ainsi l’un des rares domaines où l’on a un accès expérimental direct aux fluctuations quantiques. Le même type de mesure est beaucoup plus difficile pour le cas de particules matérielles, où les dispersions quantiques sont en général masquées par d’autres bruits de fond, par exemple par le bruit thermique. Par un retournement de situation dont la physique est coutumière, les dispersions E ¹ et E ² sur les mesures, qui sont considérées en général comme une limitation dans la connaissance du système, contiennent en fait des renseignements supplémentaires sur celui-ci. Leur détermination permet de mieux connaître l’état physique exact de l’onde.

2. Les différents types d’ondes lumineuses quantiques

À la différence de l’onde classique, dont l’état est entièrement défini par la donnée des deux paramètres réels E ¹ et E ², il existe une variété extraordinaire d’états quantiques de l’onde, qui donnent des valeurs différentes non seulement aux valeurs moyennes des grandeurs à mesurer, comme E ¹ et E ², mais aussi aux fluctuations autour de ces valeurs moyennes, ou encore aux corrélations entre différentes grandeurs mesurées. On passera ici en revue les types d’états les plus importants.

Le « vide »

Il s’agit de la dénomination traditionnelle de l’état de plus basse énergie de l’onde, que l’on pourrait appeler de manière plus appropriée l’« obscurité ». Le « vide » ne contient aucun photon. En revanche, le champ électrique dans cet état ne peut être nul en tout point et à tout instant, car sinon l’inégalité (4) serait violée. La valeur moyenne du champ est nulle, mais pas les dispersions E ¹ et E ², qui sont telles que E ¹ = E ² = E^v . Le vide est ainsi le siège de fluctuations non nulles autour de 0, appelées fluctuations du vide , dont l’existence permet de mieux comprendre de nombreux phénomènes. Par exemple, la désexcitation spontanée d’un atome initialement excité peut être considérée comme induite par les fluctuations du vide. Dans le plan de Fresnel, le vide est représenté par un cercle centré à l’origine et dont le diamètre est égal à E^v (fig. 1 c).

Les états « quasi classiques »

Dans ces états, la valeur moyenne du champ évolue sinusoïdalement, exactement comme le champ classique [équation (1)]. Le champ présente autour de cette valeur moyenne des fluctuations minimales compatibles avec la relation de Heisenberg (2), telles que E ¹ = E ² = E^v . L’état quasi classique est ainsi l’état quantique qui est le plus proche de l’onde lumineuse de la théorie classique. On peut le représenter dans le plan de Fresnel sous la forme d’un cercle de diamètre E^v centré autour d’un point M qui n’est pas l’origine (surface circulaire sur la figure 1 d). On peut montrer que l’énergie H et le nombre de photons n fluctuent eux aussi dans un état quasi classique. On obtient plus précisément les expressions:

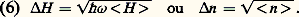La dispersion des fluctuations y est donc proportionnelle à la racine carrée de la valeur moyenne. On appelle « bruit de grenaille » (shot noise en anglais) ce type de fluctuations. C’est en effet celui qu’on entend, par exemple, lorsqu’un jet de grains de sable heurte une paroi. D’un point de vue énergétique, l’état quasi classique peut donc aussi être considéré comme un jet de « grains de lumière » indépendants les uns des autres.

Les états à n photons

Ce sont les états dont le nombre de photons est strictement égal à n (cf. PHOTONS). Leur énergie est alors parfaitement spécifiée. On a donc H = 0 et, d’après (5), une dispersion 﨏 infinie. Le champ électrique d’un état à n photons a donc une amplitude parfaitement définie et une phase aléatoire. L’état à n photons a essentiellement des propriétés « corpusculaires », mais il n’est cependant pas complètement réductible à une assemblée de n corpuscules classiques. On a en effet montré, théoriquement, puis expérimentalement dans le cas n = 1, qu’on peut observer des franges d’interférence lorsqu’on envoie un tel état dans un interféromètre. Dans ce cas, c’est le photon qui « interfère avec lui-même » par les deux chemins possibles du faisceau dans l’interféromètre.

Les états comprimés (ou « squeezés »)

Comme pour un état quasi classique, la valeur moyenne du champ électrique dans un état comprimé a une évolution sinusoïdale classique, et les fluctuations E ¹ et E ² satisfont à l’égalité dans la relation (4): E ¹ 練 E ² = E^v (fluctuations minimales compte tenu des contraintes imposées par la mécanique quantique). À la différence de l’état quasi classique, E ¹ et E ² sont différents. On a E ¹ 麗 E^v par exemple, et donc nécessairement E ² 礪 E^v . L’état est représenté dans le plan de Fresnel par l’ellipse de la figure 1 d. On voit sur la figure que les fluctuations E ⁰ de l’amplitude du champ dans cet état sont plus petites que dans l’état quasi classique. En conséquence, l’incertitude sur l’énergie, ou sur le nombre de photons (quantités proportionnelles à E ²⁰), peut être fortement réduite dans un état comprimé par rapport au bruit de grenaille n = ‘ 麗n 礪 de l’état quasi classique. Cette amélioration a évidemment un prix: il y a augmentation correspondante des fluctuations de phase 﨏 et perte de la cohérence ^{[cf. OPTIQUE - Optique cohérente]}.

Les états « chats de Schrödinger »

Pour illustrer les paradoxes de la théorie quantique, Schrödinger avait imaginé un état étrange constitué par la superposition quantique de la fonction d’onde de deux objets macroscopiques: un chat vivant et un chat mort ^{[cf. SCHRÖDINGER (E.)]}. On peut imaginer un état de la lumière qui lui ressemble beaucoup. Il est constitué par la superposition quantique du vide (le chat mort) et d’un état quasi classique comportant en moyenne un grand nombre de photons (le chat vivant). À la différence de l’état introduit par Schrödinger, il s’agit d’un objet quantique parfaitement défini dont on peut calculer les propriétés. On peut ainsi soumettre à un examen approfondi les étranges propriétés de ces états.

3. Comment produire ces différents états quantiques?

Les sources traditionnelles de lumière comme les lampes à incandescence, à arc ou à décharge produisent des états de la lumière dont les fluctuations sont essentiellement d’origine statistique (fluctuations thermiques par exemple). Si on s’intéresse uniquement aux valeurs moyennes des quantités physiques, on montre que les résultats des mesures optiques obtenues en utilisant ces sources s’expliquent en faisant appel uniquement à la théorie classique du rayonnement. Le champ électrique produit par ces sources « classiques » présente tout de même d’inévitables fluctuations d’origine quantique. On peut établir en particulier que la dispersion H sur la mesure de l’énergie H d’un faisceau lumineux « classique » satisfait à l’inégalité:

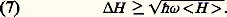En d’autres termes, les fluctuations d’intensité des faisceaux lumineux produits par des sources « classiques » sont limitées inférieurement par le bruit de grenaille de l’état quasi classique (équation 6). Ces sources étant les seules existant jusqu’aux années 1980, on a longtemps affirmé que les fluctuations d’intensité de tout faisceau lumineux ne pouvaient pas être inférieures au bruit de grenaille. Il semblait donc exister une sorte de barrière infranchissable s’opposant à l’amélioration infinie de la précision des mesures optiques. Cette limitation ne s’impose en fait que pour les faisceaux produits par les sources « habituelles » ou classiques de rayonnement. La seule barrière vraiment infranchissable est celle qui résulte des inégalités (5).

Le cas des lasers est plus complexe ^{[cf. LASERS]}: les lasers usuels obéissent à l’inégalité (7) et, dans certaines conditions, à l’égalité (6): ils peuvent donc produire des états quasi classiques pratiquement idéaux. Mais on peut faire mieux pour quelques lasers particuliers: des expériences récentes ont montré que certains lasers à semiconducteurs produisaient un faisceau lumineux comprimé, dont le bruit d’intensité était réduit d’environ un facteur 10 par rapport à la « limite » (7) du bruit de grenaille.

Par ailleurs, on a montré expérimentalement qu’on pouvait transformer un état quasi classique (produit par un laser usuel) en un état comprimé en le faisant passer dans un dispositif d’optique non linéaire, comme un oscillateur paramétrique ou un système doubleur de fréquence. On a fait aussi d’autres expériences qui montrent que les états comprimés permettent d’augmenter la sensibilité des mesures optiques en réduisant le bruit de fond au-dessous de la « limite » du bruit de grenaille, notamment dans les mesures spectroscopiques et interférométriques.

Les états à n photons sont, eux, beaucoup plus difficiles à obtenir. L’émission spontanée d’un atome initialement excité permet dans certaines conditions de produire un état à 1 photon. En revanche, jusqu’à présent, les états à n photons avec n 礪 1 ou bien les états « chats de Schrödinger » n’ont encore jamais été produits expérimentalement.

4. Mesures quantiques non destructives sur un faisceau lumineux

L’existence d’effets perturbateurs inévitables exercés par tout appareil de mesure sur l’objet à mesurer est connue depuis les débuts de la mécanique quantique (cf. mécanique QUANTIQUE, MESURE, RÉALITÉ PHYSIQUE). Ces effets n’ont été soumis à des tests expérimentaux détaillés que récemment, avec les progrès de l’optique quantique évoqués plus haut. La possibilité de mesurer par des méthodes optiques le passage sur la Terre d’ondes gravitationnelles, qui provoque d’infimes variations des longueurs (10^–18 m pour un interféromètre de 1 km de longueur!), a en particulier incité les physiciens à étudier attentivement ces problèmes. En effet, le signal qu’on peut attendre dans de telles mesures est du même ordre de grandeur que les fluctuations quantiques existant dans l’appareil de mesure.

Braginsky, en 1977, fit remarquer que la mécanique quantique n’interdisait pas l’existence de « mesures quantiques non destructives » (en abrégé: mesures « QND »), pour lesquelles la perturbation inévitable engendrée par le processus de mesure sur le système à mesurer n’affecte pas la quantité précise que l’on veut mesurer. Par exemple, il est possible de concevoir des méthodes de mesure QND de l’énergie H d’une onde lumineuse. Celles-ci permettront de mesurer l’énergie avec une incertitude H aussi petite que l’on veut. L’effet perturbateur inévitable exercé par le processus de mesure affectera alors uniquement la phase de l’onde, qui sera connue avec une incertitude 﨏 telle que: 﨏 練 H 閭 h 諸/2, c’est-à-dire d’autant plus importante que l’énergie sera connue avec précision.

La mesure la plus simple de l’énergie lumineuse, consistant à insérer un photodétecteur sur le trajet du faisceau, est évidemment une mesure « destructive » de celle-ci, puisque le faisceau n’existe plus après la mesure. On peut alors insérer une lame de verre faiblement réfléchissante (fig. 2), qui détourne sur le photodétecteur une fraction connue du faisceau et laisse passer l’essentiel de l’énergie lumineuse. L’optique quantique montre que ce dispositif réalise lui aussi une mesure destructive de l’intensité lumineuse, car il modifie la valeur précise de l’intensité du faisceau émergeant du dispositif. Ce résultat, en apparence paradoxal, provient du fait que la lame de verre couple au faisceau sortant une autre onde lumineuse: celle qui se réfléchit sur l’autre côté de la lame (fig. 2). L’état quantique de cette onde est précisément le vide, qui, comme nous l’avons vu, présente des fluctuations non nulles qui vont perturber le faisceau de sortie.

Pour réaliser une mesure QND, il faut donc réaliser des dispositifs plus complexes. On peut, par exemple, envoyer sur la seconde voie d’entrée de la lame de la figure 2 un faisceau lumineux comprimé, ayant des fluctuations inférieures à celles du vide sur la composante de quadrature E ¹. On aura alors un dispositif permettant de faire une mesure quantique non destructive de cette composante de quadrature du champ, la perturbation due à la mesure étant reportée sur la composante E ² dont les fluctuations E ² auront été augmentées.

Récemment, des équipes de chercheurs dans le monde ont réalisé des dispositifs de mesure QND, en utilisant différentes méthodes d’optique non linéaire.

Par souci de simplicité, cet article se restreint volontairement à la description quantique d’une onde monochromatique unique. D’autres effets quantiques surgissent lorsqu’on s’intéresse à des configurations plus compliquées. On peut, par exemple, produire par des méthodes d’optique non linéaire deux faisceaux lumineux présentant des corrélations quantiques parfaites : la mesure d’une grandeur sur l’un de ces faisceaux donne immédiatement des renseignements sur l’état exact de l’autre faisceau. Ce dispositif a permis de prouver expérimentalement le caractère non local du monde quantique ^{[cf. RÉALITÉ PHYSIQUE]}. La prise en considération de la polarisation de la lumière conduit aussi à des effets quantiques intéressants, utilisés en cryptographie quantique . Dans ce type de dispositif, ce sont les lois quantiques de la mesure qui empêchent tout espion, aussi astucieux soit-il, de prendre connaissance du message sans se faire lui-même reconnaître. Ces quelques exemples montrent toute la richesse des développements actuels de l’optique quantique.

Encyclopédie Universelle. 2012.